Find Values of a and B That Make F Continuous and Differentiable Over Entire Domain
Find all values of $a$ and $b$ that make the following function differentiable for all values of $x$
Solution 1
The only value of $x$ that gives any trouble is $x=-1$. You want $f$ to be continuous there, which gives you one equation in $a$ and $b$, and you want it to have the same derivative whichever formula you use, and that gives you a second equation.
Solution 2
The two "pieces" of $f(x)$ are pleasantly smooth. The only potential source of problems is at $x=-1$, where the pieces join up nicely, we hope.
So first of all, $f(x)$ must be continuous at $-1$. This will be the case if the limit of $ax+b$, as $x$ approaches $-1$ from the right, is the same as the limit of $bx^2-3$, as $x$ approaches $-1$ from the left.
That comes down to saying that $-a+b=b-3$. We conclude that for continuity of $f(x)$ at $x=-1$, we must have $a=3$.
But continuity does not imply differentiability: the two pieces of $f(x)$ must not only join up nicely, they must join up without a "kink." We can make sure of this by making sure that the limit of the slope of $ax+b$, as $x$ approaches $-1$ from the right, matches the limit of the slope of $bx^2-3$, as $x$ approaches $-1$ from the left.
The slope of $ax+b$ is always $a$, that is, always $3$. So we want the slope of $bx^2-3$ to approach $3$ as $x$ approaches $-1$ from the left.
The derivative of $bx^2-3$ at $x$ is $2bx$, which approaches $-2b$ as $x$ approaches $-1$ from the left. So we want $-2b=3$.
Another approach is to imagine two full curves, $y=p(x)=ax+b$ and $y=q(x)=bx^2-3$. We want to be able to travel rightward along $y=bx^2-3$ and then at $x=-1$ smoothly enter the curve $y=ax+b$, without jump or bump. That means that (i) The functions must match at $-1$, so $p(-1)=q(-1)$ and (ii) Their derivatives match at $-1$, so $p'(-1)=q'(-1)$. The rest of the calculation is the same as in the first version of the solution.
Comment: In computer graphics, simple functions defined over shortish intervals are used to produce more complex shapes. For the simple functions, cubics are often good enough, one might even try for quadratics. Then we have to make sure that the cubic or quadratic pieces join up smoothly. Certainly we want continuity at the joins, but also differentiability, and preferably twice differentiability. For more information about this, one keyword is splines.
Solution 3
The two expressions are differentiable everywhere. So you only have to test where they meet, that is, at $x=-1$. You want the derivatives at $x=-1$ to match. You also want the function to be continuous at $x=-1$. That gives you two equations and you can solve for $a$ and $b$.
Related videos on Youtube
Comments
-
Problem
Find all values of $a$ and $b$ that make the following function differentiable for all values of $x$: $$ f(x) = \begin{cases} ax + b, x > - 1\\ bx^2 - 3, x \leq -1\\ \end{cases} $$I was reviewing all my works for the last 3 years, and suddenly I found this problem in one of my homework assignment. Unfortunately, this assignment lacks the solution. I was 100% sure that I used to solve it correctly, but without a textbook I couldn't recall my poor memory. I knew this is a very basic question for the first calculus course, but I totally forgot how to start, could anyone give me a "tiny" hint? Thank you.
-
Myerson: Ah ha, great thanks. I remember it now ;)
-
This answer could add commentary as to why this technique could/should work, rather than making the approach seem like black magic.
-
If you plug in $-1$ for $x$ in both equations in my exam you get a zero... continuity needs $\lim_{x\rightarrow a}f(x)=f(a)$ and while you "recipe" appears to calculate the left- and right-hand limits it does so implicitly rather than explicitly which can run into problems. For example what would you do with $\displaystyle f(x):=\left\{\begin{array}{cc}x+a &\text{ if }x<0\\ 4&\text{if }x=0\\ b-x&\text{ if }x>0\end{array}\right.$
Recents
constantanium1957.blogspot.com
Source: https://9to5science.com/find-all-values-of-a-and-b-that-make-the-following-function-differentiable-for-all-values-of-x



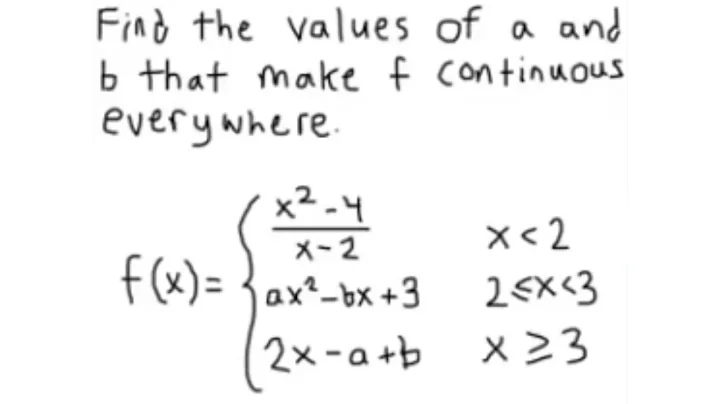

0 Response to "Find Values of a and B That Make F Continuous and Differentiable Over Entire Domain"
Post a Comment